
Editor’s Note: The following is an article originally published on the author’s Substack Heterodox STEM on October 14, 2025. With edits to match Minding the Campus’s style guidelines, it is crossposted here with permission.
The American Association of University Professors (AAUP), proudly trumpeting its obscurantism, has pre-published “Seven Theses Against Viewpoint Diversity: The problems with arguments for intellectual pluralism.” These theses boil down to “some thoughts are wrong,” which is true but woefully incomplete. They ignore the greatest merit of viewpoint diversity, namely that it speeds social learning. This conclusion, which follows easily from Bayes’ rule, is analogous to Fisher’s Fundamental Theorem of Natural Selection in evolutionary biology. Genetic diversity is crucial to the quest for biological fitness. Viewpoint diversity is crucial to the quest for truth.
Here are author Lisa Siraganian’s seven theses, with my brief retorts alongside:
- Viewpoint diversity functions in direct opposition to the pursuit of truth, the principal aim of academia. Actually, truth is often discovered through opposition to consensus falsehoods.
- Viewpoint diversity can work only as an instrumental value. Nothing wrong with that. Food is instrumental to life, even though it is accompanied by defecation.
- Viewpoint diversity assumes a partisan goal based on unproven assumptions. Only partisans assume that their own assumptions are proven by assertion and that others’ goals are partisan.
- Viewpoint diversity undermines disciplinary and specialized knowledge and standards as well as the autonomy of academic reasoning and scholarship. Tell that to the patent clerk who propounded the theory of relativity.
- Viewpoint diversity is incoherent. Yes, diversity often pits two views against each other. COVID-19 either arose in a Chinese lab or didn’t.
- Viewpoint diversity has already been used, both in the United States and abroad, to attack higher education and stifle academic freedom. So has opposition to viewpoint diversity.
- Viewpoint diversity is an argument made in bad faith. Bad faith protects the positions and privileges of people whose arguments cannot stand real scrutiny.
What bothers me most about these theses is what they leave out: any mention of uncertainty or doubt. The great physicist Feynman identified science as a “culture of doubt.” He said, “I would rather have equations that can’t be answered than answers that can’t be questioned.” He warned, “The first principle is that you must not fool yourself and you are the easiest person to fool.” Professor Siraganian’s polemic never acknowledges that academic consensus can be fooled. Yet the woke scholarship seemingly dearest to AAUP leaders regularly contemns prior consensus and predecessors’ supposed foolishness. Did truth only emerge when they sought tenure?
To offer an olive branch, I will endorse all the professor’s theses if she will change half a word. Replace “viewpoint” with “viewed” and they make perfect sense. Why should viewed diversity—skin color, facial appearance, presentation as man or woman—have any bearing on the quest for truth? In practice, viewed diversity doesn’t even promote viewpoint diversity, although advocates often claim that it does.
[RELATED: Faculty Face Widespread Punishment for Speech, Administrators and Unions Stay Silent]
Natural Selection
The struggle for academic truth resembles natural selection in biology. The fittest views or organisms tend to survive best, but there is a lot of turmoil along the way. It might seem better to converge on a single best path and stay there. Yet a single path might be too rigid to respond to new questions or environmental challenges. How do we reconcile fitness with variation?
This question rattled evolutionary biologists for decades. Darwin thought inheritance occurred through pangenesis, whereby sperm captures all the father’s traits, eggs capture all the mother’s traits, and fertilization blends them together. Under pangenesis, reproduction generates averages of averages. This tends to smother variation unless pangenesis adds a lot of noise, and if it adds a lot of noise, then successful reproduction should be rare.
In contrast, Mendelian genetics easily accounted for sustained variation. Each organism carries many pairs of trait-determining genes, with each gene in the pair inherited from a different parent. While one gene typically dominates in expression, the two genes are equally likely to get transmitted to offspring. In this way, sexual reproduction preserves variation from one generation to the next. However, preservation of variation seemed to impede the evolutionary quest for fitness.
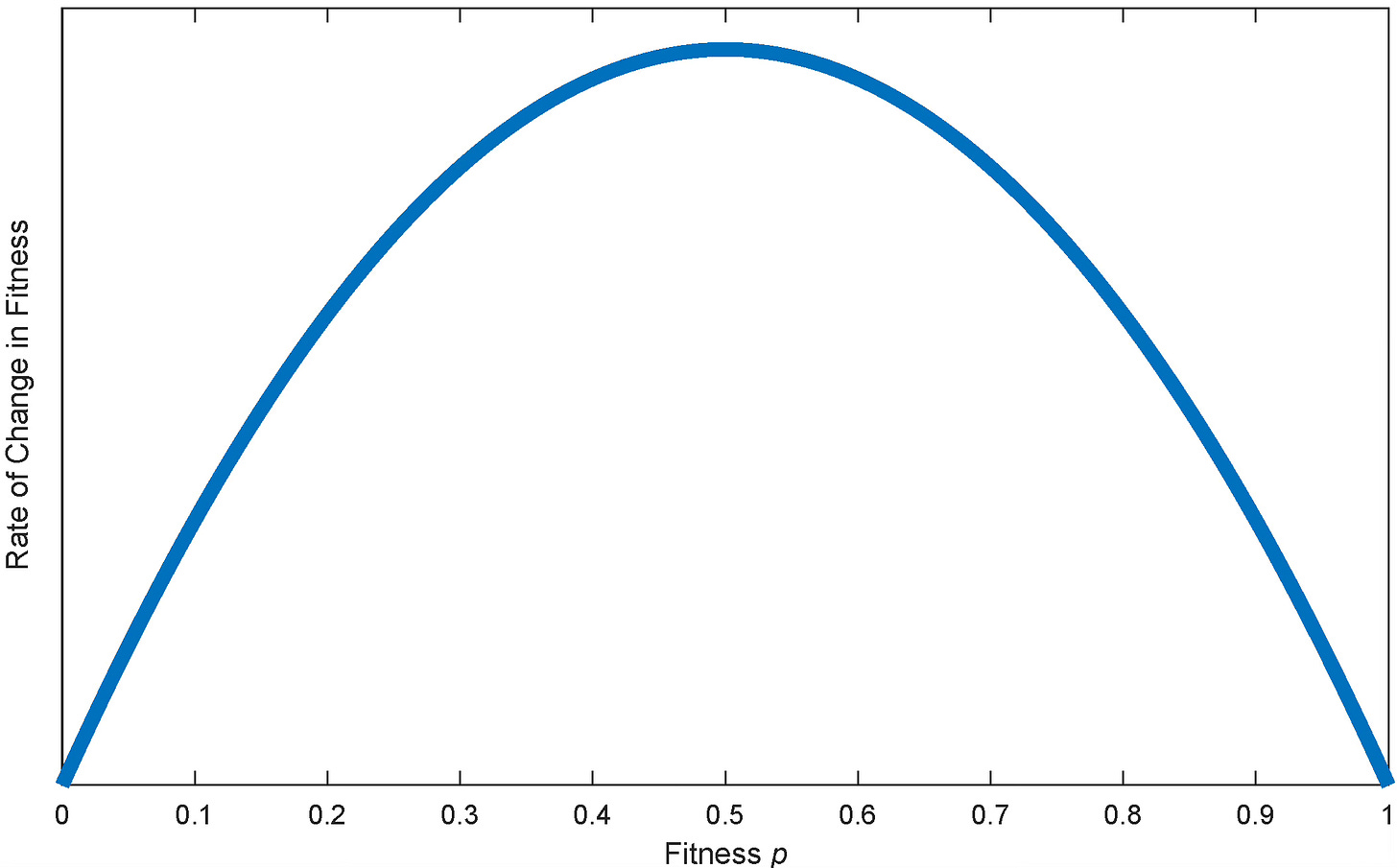
The split was resolved by Ronald Fisher, arguably the greatest of Darwin’s successors and also a giant in statistics. He called the resolution the “fundamental theorem of natural selection” and stated it as follows: “The rate of increase in any organism at any time is equal to its genetic variance in fitness at that time.”
To understand its gist, consider two competing genes in proportions p and 1-p. Suppose that the first gene outcompetes the second at rate α. It is readily shown that p tends to increase at rate αV, where V=p(1-p) denotes the variance. The figure below charts the expected improvement rate as a function of fitness. To be clear, this depicts a statistical regularity rather than a deterministic outcome. Static environments favor static fitness with low variance; we want p close to 1 for the best genes. Unstable environments favor robust adaptation, which is best served by high variance. Taleb explains it very well, albeit under a new name “antifragility” and without crediting Fisher.
[Related: Universities Have a Logic Problem]
Rational Learning from Experience
There are some truths we can be sure of. We know, for example, that the ratio of a perfect circle to its diameter is π, even though it is hard to figure out the value of π. But the imperfections of real-life circles invite debate. For another example, we know a lot about how perfectly fair coins behave, but no one knows whether a given coin is perfectly fair.
The scientific study of uncertainty is founded on probabilistic modeling and Bayes’ rule. Probabilistic modeling treats each possible chance θ of heads as a hypothesis with probability p(θ) of being true. Bayes’ rule updates each p(θ) after an observed outcome x in proportion to the chance that the given θ would generate x.
Conceptually, the Bayesian approach applies to nearly all learning from experience. Consider the proposition “Y causes Z.” No plausible explanation and host of Y-followed-by-Z events fully proves that, since it is hard to rule out all related factors and impossible to know whether we have considered all relevant contexts. Some degree of doubt remains, unless we simply deny it. Granted, all of us ignore some doubts, aka round them to zero, as no brain can handle infinite clutter. But no one should prohibit all tiny doubts, which sometimes deserve to grow big.
Here is a simple example. A coin is tossed 10,000 times with equal numbers of heads and tails and no strikingly unusual patterns. Fair price for a bet that pays 1 for heads and 0 for tails is very close to 0.5. Suddenly, the coin starts landing heads at every toss. How many straight heads would you need to observe before estimating a fair price E of 0.9?
If you say 40,000, you have failed a Turing test for human intelligence. Don’t worry, though, you’re in good company. That’s what all the LLMs I asked in February 2025 initially answered. They implicitly presumed that all tosses are independent and identically distributed (IID). No human should fail to suspect that IID failed. Perhaps the coin got switched. Perhaps the tosses were rigged. Perhaps the reporting was fraudulent.
Once we factor in tiny doubts, say a 1 in a million chance of fraud, the response pattern looks very different. A few dozen heads in a row usually suffice to make us openly wary. From there, 8-10 more heads usually motivate a 9-to-1 bet on heads. But the details vary enormously with the type and intensity of doubts. Some variants are pictured below. None of them are unreasonable but sometimes they strongly disagree; some can be 95 percent or more convinced the coin is fair while others are 95 percent or more convinced it isn’t. You can read the mathematical details here.

How consensus gets formed under these conditions is a fascinating topic, and the answer helps explain financial markets’ vulnerability to turbulence. But here I want to focus on one thing only. Why does the same evidence—in this case, one more head—affect mean beliefs E so much more in some contexts than others? The answer is that E responds to the product of unexpected news and the variance V of beliefs. The math is analogous to Fisher’s Fundamental Theorem with an analogous conclusion: “Rational learning is generally fastest when the variance of beliefs is highest.”
A Case Study
As the relation between changes in mean beliefs and variance is a mathematical truth, AAUP’s opinion on it doesn’t matter. However, there are empirical questions about how much rational learning real-life professors really do. Here is a case study.
Medical professors in 1840s Vienna prided themselves on their skill and know-how, some of it honed through practice with cadavers. Yet the esteemed maternity clinic they staffed had a much higher rate of postpartum infection and death than the lesser clinic run by midwives. Pregnant women were said to go into labor on the street in order to secure emergency treatment by midwives instead of doctors.
A young doctor, Ignaz Semmelweis, was hired to assist the hospital administration. After accidentally stabbing a friend with an unclean scalpel during an autopsy—and watching him die from the same infection killing new mothers—Semmelweis concluded that “cadaverous particles” were the cause. He then insisted that doctors wash their hands in a chlorine solution—chosen partly for its strong smell—between autopsies and patient examinations. Mortality rates plunged.
However, the esteemed doctors took offense. They felt insulted by aspersions on their cleanliness. Furthermore, germ theory had not yet been developed; the established theories of disease emphasized internal imbalances of bodily fluids. Semmelweis was dismissed and forced to move to Budapest, where he started writing open letters. Increasingly angry, he denounced the medical establishment as murderers for not applying his methods broadly, while his personal behavior grew more erratic. Eventually, he was committed, with his wife’s assent, to a lunatic asylum where he was severely beaten by guards and died of sepsis.
For two decades, Semmelweis’s advice made only slow headway. The great majority rejected it; variance was low. Antiseptic use spread much faster once germ theory gained traction and undermined faith in older theories. Semmelweis is now lauded as a pioneer, and the kneejerk tendency to reject new evidence that contradicts established norms is known as the “Semmelweis reflex.”
How does Semmelweis rate on Siraganian’s metrics? Terribly. He opposed an established norm. He made unproven assumptions that weren’t fully coherent. He criticized recognized experts and denied them respect. He was accused of bad faith. But Semmelweis saved many mothers’ lives and could have saved more had he not been quickly and contemptuously dismissed.
Shame on AAUP for siding with convention over conflict, with denigration over debate. Groupthink deters great thinking.
Image by Stefan on Adobe; Asset ID#: 507165772